Ключова разлика : В смятането диференциацията е процесът, чрез който се определя скоростта на промяна на кривата. Интеграцията е точно обратното на диференциацията. Обобщава цялата малка площ, разположена под крива, и открива общата площ.

Диференциацията и интеграцията са два градивни елемента на смятане. Диференциалното смятане и интегралното смятане са точно една от друга. Диференциалното смятане се занимава основно с процеса на разделяне, за да се проследи промените. От друга страна, интегралното смятане добавя всички парчета заедно.

Диференциацията се занимава с изчисляването на дериватив, който е моментната скорост на промяна на функцията, взета под внимание в една от нейните променливи. Той се занимава с количества, които непрекъснато варират. С други думи, тя е еквивалентна на наклона на допирателната линия, която е представена с m = промяна в y / промяна в x.

Може да се разбере от този пример - ако съществува функция f (x), притежаваща независима променлива x, то в случай, че x се увеличи с малко количество, което би било делта x. Тогава същата промяна ще бъде отразена във функцията също като delta f. Съотношението делта f / делта х изчислява скоростта на промяна на функцията по отношение на променливата х.

Интеграцията е точно обратното на диференциацията и следователно също се нарича анти-диференциация. Той е в състояние да определи функцията, която е нейната производна. Той измерва площта под функцията между границите. Процесът на интеграция е безкрайното сумиране на произведението на функция x, която е f (x) и много малка делта x. В контекста на крива, тя осигурява общата площ под кривата от оста x до кривата от определен диапазон. Тя е изобразена със символа. Ако специфичният интервал е споменат, то той е известен като определен интеграл, иначе неопределен интеграл.

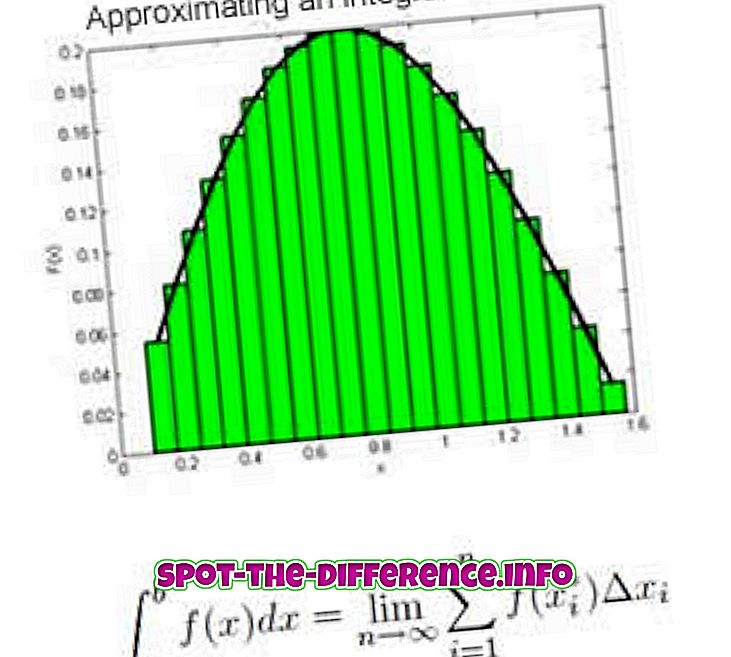
Тъй като интеграцията и диференциацията са само една от друга, интеграцията може да осигури оригиналната функция, ако е известна деривация. Тя също е описана като основна теорема за смятане. Диференциалите са свързани с различия и разделения, докато интеграцията е свързана само с добавянето и усредняването. Диференциалът определя функцията на наклона, тъй като разстоянието между две точки става много малко, подобно на процеса на интеграция се определя площта под кривата, тъй като броят на преградите, разположени под кривата, става голям.

Сравнение между диференциация и интеграция:

	разграничаване	интеграция
разлика	Използва се за намиране на промяната във функцията по отношение на промяната на входа	Обратен процес или метод на диференциация
Базиран на	Разделяне	Интегриране
Определя	Скорост на функцията	Разстояние, изминато от функцията
диаграма	Наклон на функцията	Област между функцията и оста х
пример	За у = х към силата на 4 dy / dx = 4 (x повишаване до 3)	Интеграцията на 4 (x рейз до силата на 3) е равна на = x към силата на 4
формула	Производната на функция f (x) по отношение на променливата x се определя като	Определението за интеграла на f (x) от [a, b]
Приложение	За да се определи дадена функция се увеличава или намалява, изчисляване на моментната скорост	Използва се за намиране на области, обеми, централни точки и др