Ключова разлика: А кръг и елипса са затворени извити форми. В кръг всички точки са еднакво отдалечени от центъра, което не е случаят с елипса; в елипса всички точки са на различни разстояния от центъра.
Математически, окръжност е основна форма в областта на геометрията и нейното определение е: кръг е форма с всички точки на същото разстояние от неговия център. Нарича се от центъра му. Някои реални примери за кръг са колела, чиния и (на повърхността) монета.
Думата " цирк " произлиза от гръцкия термин " kirkos ", който е метатеза на хомерския гръцки и означава " обръч " или " пръстен ". Кръгът е известен преди записаната история. Слънцето и Луната са естествени примери за кръг, докато дори къс дръжката, която духа на вятъра, оформя формата на кръг в пясъка. Принципът на кръга се прилага при формирането на колела и предавки от праисторическия човек. Сега в съвременната ера съществуват множество видове машини, базирани на формата на кръга. Изучаването на кръг и неговото развитие е приложимо в областта на математиката, геометрията, астрономията и смятането.
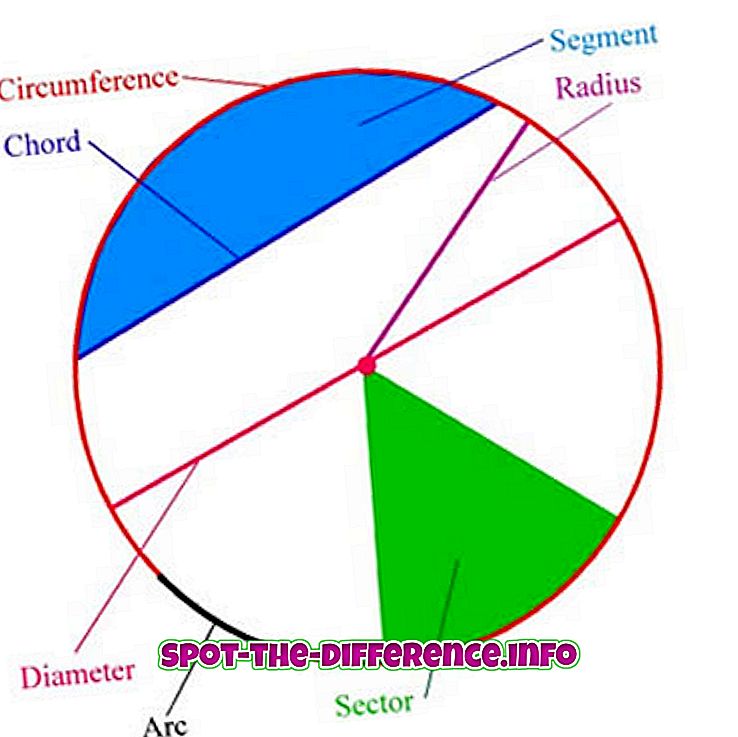
Следните термини са включени в кръговата терминология:
Дъга : всяка свързана част от кръга.
Център : точката, която е на еднакво разстояние от точките в кръга.
Радиус : линия, свързваща центъра на кръга с всяка точка на самия кръг; или дължината на такъв сегмент, който е половин диаметър.
Диаметър : линеен сегмент, чиито крайни точки лежат върху кръга и преминават през центъра; или дължината на такъв линеен сегмент, който е най-голямото разстояние между две точки на окръжността. Това е специален случай на акорд, а именно най-дългият акорд и е два пъти радиуса.
Обхват e: дължината на една верига по окръжността.
Chord : линията, чиито крайни точки лежат върху кръга.
Допирателна : Копланарна права линия, която докосва кръга в една точка.
Полуоколо e: област, ограничена от диаметър и дъга, разположена между крайните точки на диаметъра. Това е специален случай на кръгов сегмент, а именно най-големият.
Кръгов сектор : област, ограничена от два радиуса и дъга, разположена между радиусите.
Математически, елипсата е обща форма в областта на математиката. Неговата дефиниция гласи: крива линия, образуваща затворен контур, където сумата от разстоянията от две точки (огнища) до всяка точка на линията е постоянна. Примерите за реалния живот на елипсата са: обръч на хула, чаша вода и проста табела за вечеря, когато се накланя, за да се види под ъгъл.
Аполон от Перга дава името „елипса“ в своята Коника, което подчертава връзката на крива с приложението на области. Това е крива на равнина, която заобикаля две фокусни точки, така че права линия, изтеглена от една от фокалните точки до която и да е точка на кривата, а след това обратно до другата фокусна точка, има същата дължина за всяка точка на кривата. Неговата форма е представена от неговия ексцентричност, която е произволно близка до 1. Изследването на елипсата и нейните свойства са общо приложими в областта на физиката, астрономията и инженерството. Орбитите на планетите със Слънцето в една от фокалните точки, спътниците, които обикалят около планетите, и други системи, имащи два астрономически тела, са общите примери за елиптични пътеки. Формата на планетите и звездите често е добре описана от елипсоиди. Елипсата също се счита за най-простата фигура на Лисажу, образувана, когато хоризонталните и вертикалните движения са синусоиди със същата честота.
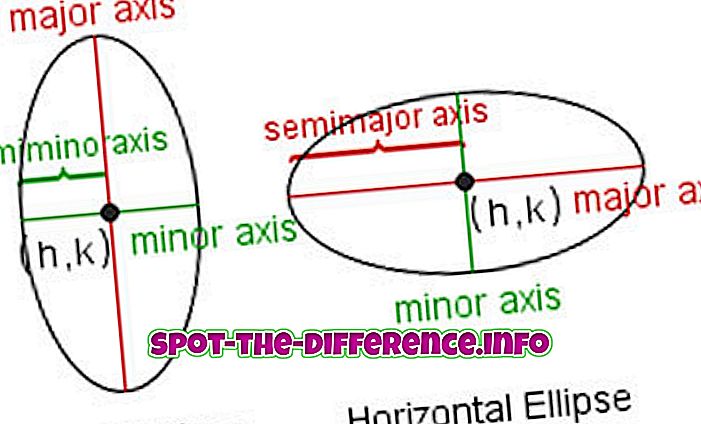
Термините, използвани главно в терминологията на елипсата, са:
Фокус : Разстоянието от центъра и се изразява в големи и малки радиуси.
Ексцентричност : Ексцентрицитетът на елипсата (обикновено означен или като e или ε) се изразява чрез използване на коефициента на сплескване.
Directrix : тя е линия, успоредна на малката ос и с която всеки фокус е свързан.
Latus rectum : Акордите на елипса, които са перпендикулярни на главната ос и преминават през един от нейните огнища, се наричат latus rectum на елипсата.
Основна / малка ос : Най-дългият и най-къс диаметър на елипсата. Дължината на главната ос е равна на сумата от двете генераторни линии.
Полуосновна / полу-малка ос : Разстоянието от центъра до най-отдалечената и най-близката точка на елипсата. Половината от главната / второстепенната ос.
Акорди : Средните точки на набор от паралелни акорди на елипса са колинеарни.
Обикновеност : тя е свързана с дължината на полу-главната ос и ексцентрицитета и е неразделна част от елипсата.
Сравнение между кръг и елипса:
кръг | елипса | |
Определения | Кръгът е кръгла плоска фигура, чиято граница (обиколката) се състои от точки, еквидистантни от фиксирана точка (центъра). | Елипсата е правилна овална форма, проследена от точка, движеща се в равнината, така че сумата от нейните разстояния от две други точки (огнища) е постоянна, или се получава, когато конус се срязва от наклонена равнина, което прави не пресичат основата. |
Вариации | Кръговете не се различават по форма; те остават една и съща форма, дори когато изгледът се променя. | Елипсите се различават по форма от много широки и плоски до почти кръгли, в зависимост от това колко далеч са фокусите един от друг. |
Последователност на радиуса | Той има постоянен радиус в цялата форма. | Той няма постоянен радиус в цялата форма. |
Главни компоненти | Кръгът има един радиус, който се намира в центъра. | Елипсата има два огнища, които са в двата края. |
■ площ | π × r ^ 2 Където "r" е радиусът на окръжността. | π × a × b Където "а" е дължината на полуосевата ос, а "b" е дължината на полу-малката ос. |
Стандартни уравнения | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
прилика | Кръговете са уникалните форми, от които произлизат другите форми. | Елипсите също възникват като образи на кръг при паралелна проекция и ограничени случаи на перспективна проекция. |