Ключова разлика: Параболата е конична секция, която се създава, когато равнината отрязва конична повърхност, успоредна на страната на конуса. Хипербола се създава, когато равнината отрязва конична повърхност, успоредна на оста.

Парабола и хипербола са две различни думи, раздели и уравнения, които се използват в математиката за описание на две различни части на конус. Те са различни по форма, размер и различни други фактори, включително формули, които се използват за изчисляването му. За да ги разберем, нека първо разберем конуса и различните конични участъци.

Коничното сечение е крива, която се получава, когато равнината се пресича с конус по различни различни начини. Прорезите, които се получават от пресичането, включват елипса, кръг, парабола и хипербола. Според аналитичната геометрия конусът се дефинира като „равнинна алгебрична крива на степен 2.” Популярното определение на коничната секция включва точка на фокусиране, линия на directrix и ексцентричност. Точката на фокусиране и линиите на directrix се очаква да бъдат във фиксирана дажба в конична форма. Съотношението е известно като ексцентричност на коничната част. Ексцентричността на елипсите, параболите и хиперболите се различават; елипсите имат ексцентричност по-малка от 1, параболите имат ексцентричност, която е равна на 1 и хиперболите имат ексцентричност по-голяма от 1. Най-ранната известна работа върху коничните секции може да бъде датирана от четвърти век преди Христа от Menaechmus, който открил начин да се реши проблемът с удвояването на куба чрез използването на парабола.

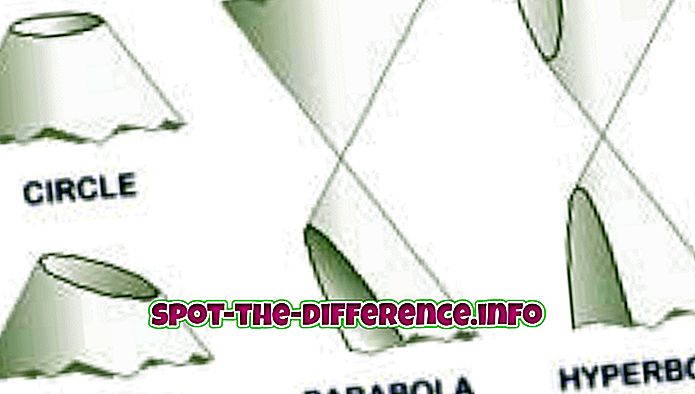
Параболата е конична секция, която се създава, когато равнината се пресича с конус. Параболите или параболите образуват „от пресечната точка на дясната кръгова конична повърхност и равнината, успоредна на генериращата права линия на тази повърхност“. Друг начин, по който се създава парабола, е когато локус от точки на равнина, които са равноотстоящи от фокуса, и директорията създават парабола. В алгебра, parabolas обикновено се използват в графики на квадратични функции, като се използва формулата y = x ^ 2.

Линията, която разделя параболата през средата, е известна като оста на симетрия; тази линия също е перпендикулярна на directrix и преминава през фокуса. Точките, които се намират на оста на симетрия, които пресичат параболата, се наричат ​​"върхове". Разстоянието между върха и фокуса е известно като "фокусно разстояние". Parabolas може да се отваря в двете посоки, включително нагоре, надолу, надясно или наляво. Също така основна черта на параболите е, че те са еднакви, само се различават по размер. Те могат да бъдат препозиционирани и пренастроени точно, за да отговарят на всяка друга парабола. Parabolas се използват в различни приложения като автомобилни светлоотразители, дизайн на балистични ракети и др. Те също играят важна роля във физиката, инженерството, математиката и др.

Хиперболите са гладка крива, която се появява, когато равнината се пресича с конуса, успореден на оста y, която създава разрез по протежение на страната на конуса. Хиперболата се определя от нейните геометрични свойства или уравнения, за които тя е набор от решения. Терминът „хипербола“ произлиза от гръцката дума, която означава „прекалено хвърлена“ или „прекомерна“. Смята се, че терминът е измислен от Аполон от Перга, който е допринесъл значително за изучаването на коничните участъци.

Известно е, че хиперболата има клони, които са огледални образи един към друг и приличат на два безкрайни лъка. Точките на двата клона, които са най-близо един до друг, се наричат ​​върхове. Линията, която свързва върховете, е известна като напречната ос или главната ос, която съответства на главния диаметър на елипсата. Средната точка на напречната ос е известна като центъра на хиперболата. Уравнението на хипербола се записва като x2 / a2- y2 / b2 = 1. Хиперболите се използват в различни приложения в днешния свят, включително пътя, последван от сянката на върха на слънчев часовник, формата на отворена орбита; използва се като арка в много построени сгради, като уравнения по математика и геометрия, физика и др.

Хиперболите и параболите са двете отворени криви, което означава, че те не завършват и продължават безкрайно до безкрайност, нещо, което елипсите и кръговете не могат да направят.