Ключова разлика: В математиката се използва уравнение, което означава равенство между две изрази. Функцията, от друга страна, е много по-сложна, отколкото уравнението. Функция се използва за означаване на връзка между набор от входове и набор от съответни изходи.

Уравнение и функция са две от основните основи на алгебрата, предмет по математика. И двете могат да бъдат доста сложни по своя характер, но в основната си форма те могат да бъдат объркани един с друг. Основната разлика между уравнение и функция е фактът, че уравнението обикновено се занимава с един вход, докато функцията може да има множество входове.

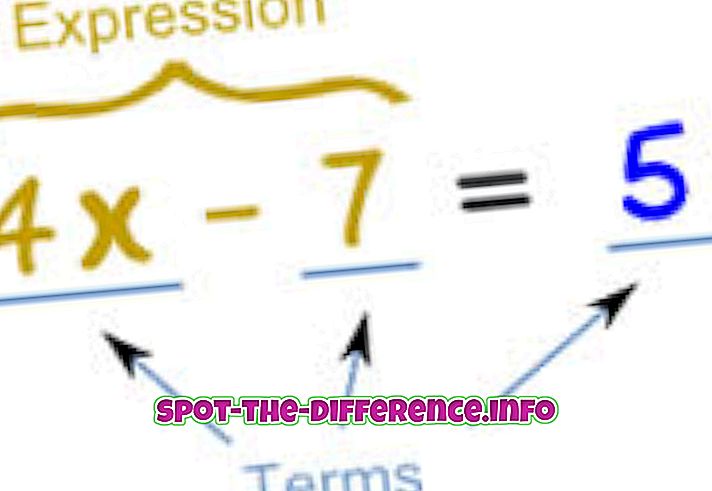
В математиката се използва уравнение, което означава равенство между две изрази. По същество уравнението се записва като израз, равен на друг израз. Например: x + 2 = 5. Това означава, че каквото и да е x, ако добавите 2 към него, ще бъде равно на 5. Следователно, можем да решим уравнението за x, което е 3, като 3 + 2 = 5.

Уравненията могат да бъдат по-сложни от това и могат да включват повече от една променлива, като x, y, z и т.н. в едно уравнение. Например: 3x + 2y - z = 4. Всяка азбука ще съответства на един номер. В този случай х = 1, у = 2 и z = 3.

Следователно,

3x + 2y - z = 4 става

3 (1) + 2 (2) - 3 = 4, което е

3 + 4 - 3 = 4 по същество

4 = 4

Функцията, от друга страна, е много по-сложна, отколкото уравнението. Функция се използва за означаване на връзка между набор от входове и набор от съответни изходи. По същество входът трябва да дава един изход. Функцията е връзка между две променливи. Например: f (x) = x + 2. Според тази функция, каквото и да е, входът е, той ще ви даде единичен изход, който ще бъде вход плюс 2. Да решим тази функция:

Вход	функция	продукция
х	f (x) = x + 2	е (х)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

И така нататък…

Функциите имат различни приложения в математиката, физиката, компютърните науки и т.н. Те могат да варират от проста функция, както е посочено по-горе, до сложни формули или алгоритми. Функцията може да се разглежда като машина, която дава изход за вход, и че изходът е някак си свързан с входа.

Функцията винаги има три части: входа, връзката и изхода. Класическият начин на писане на функция е с "f (x) = ...", където х означава входа и f (x) означава изхода.

Както е посочено по-горе, основната разлика между уравнение и функция е, че уравнението обикновено има само един вход, който ще доведе до равенство на изразите. Като има предвид, че функцията има различни входове, всяка от които ще даде изход.